引入
给出 $dq$ 轴同步旋转参考系下的 PMSM 电流方程$^{[1]}$:
$$
\begin{equation}
\begin{split}
\begin{cases}
\frac{\mathrm{d} i_{d} }{\mathrm{d} t} = -\frac{R_{s}}{L_{d}} i_{d} + \frac{\omega_{e}L_{q}}{L_{d}} i_{q} + \frac{1}{L_{d}} u_{d} \\
\frac{\mathrm{d} i_{q} }{\mathrm{d} t} = -\frac{R_{s}}{L_{q}} i_{q} - \frac{\omega_{e}L_{d}}{L_{q}} i_{d} - \frac{\omega_{e}\psi_{f}}{L_{q}} + \frac{1}{L_{q}} u_{q}
\end{cases}\\
\end{split}
\end{equation}
$$
其中,$i_d$ 和 $u_d$ 分别为 $d$ 轴的定子电流和电压,$i_q$ 和 $u_q$ 分别为 $q$ 轴的定子电流和电压,$R_s$ 为定子相电阻,$\omega_e$ 为转子电角速度,其值等于转子机械角速度 $\omega_m$ 乘以极对数 $n_p$,$\psi_f$ 为永磁体磁链常数,$L_d$ 和 $L_q$ 分别代表 $d$ 轴和 $q$ 轴的定子电感。对于表贴式永磁同步电机,可近似认为 $L_d=L_q=L_s$。
通常情况下,我们在电流环、速度环中较多使用 PI 控制器,并且在辨识得到相对准确的相电阻、电感参数的前提下,PI 控制器的参数整定已有相对较成熟的理论推导$^{[2][3]}$,对于表贴式永磁同步电机的电流环,通常有:
$$
\begin{equation}
\begin{split}
\begin{cases}
K_{p} = \frac{\omega_{b}L_{q}}{6X_{i}^2} \\
K_{i} = \frac{\omega_{b}R_{s}}{6X_{i}^2}
\end{cases}\\
\end{split}
\end{equation}
$$
其中 $K_{p}$ 为 $dq$ 轴电流环 PI 控制器的比例增益,$K_{i}$ 为 $dq$ 轴电流环 PI 控制器的积分增益,$\omega_{b}$ 为电流环的带宽,一般取 1000Hz 左右,而 $X_{i}$ 为阻尼系数,通常取 0.707。不同的文献中对于分母 $6X_{i}^2$ 的描述不同,此处为经验系数。
然而,工程实践已经证明,传统的 PI 控制器应用在速度环中时,对于阶跃信号输入存在着较大的超调量;若要降低超调量,就要在系统响应速度上做出取舍。此外,较大的积分增益也会引入积分饱和,降低系统的动态性能$^{[4]}$。对于电流环,PI 控制器的响应速度尚可接受;然而,对于电机长时间运行发热所导致的参数失配、运行过程中的外加扰动以及高次谐波电流等问题(特别是 $d$ 轴),PI 控制器的调节效果就有值得改善的空间了。
为得到更好的控制效果,引入 ADRC 控制器。基本概念:通过扩张状态观测器 ESO(Extended State Observer),实时对总扰动进行观测估计,并在输入端进行补偿,使得被控对象表现得像一个理想模型,即积分串联标准性(尽管被控对象实际动态特性并非如此)$^{[5]}$。
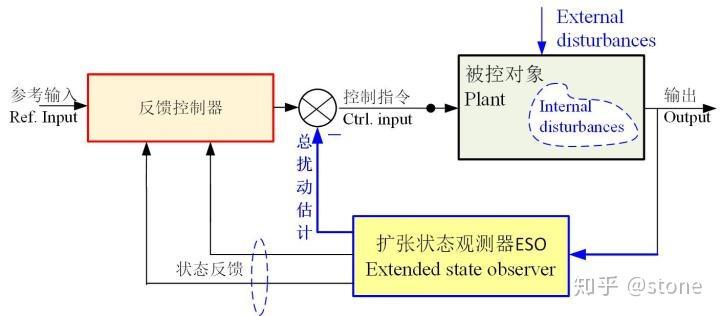
事实上,ADRC 作为一种不依赖模型的控制方法,其低阶线性版本自然就和同样不依赖于系统模型的 PID 控制器存在某种对应关系$^{[5][6]}$,厦门大学的金辉宇老师$^{[7]}$已经推导出低阶 LADRC 控制器与 PID 的等效形式:
由此可见二阶 LADRC 可以等效为 PID 控制器串联一个没有零点的二阶低通滤波,显然该滤波器是由 Luenberger 形式的 ESO 引起。
那么与 PID 相比,LADRC 的优势异常显著:
- $C_{FL}(s)$ 的低通特性可以滤掉高频的未建模动态,防止 PID 控制器在高频段将这些动态放大,从而避免引起高频的振荡。
这就是 LADRC 相对于 PID 最大的优势,也是 LADRC 工程实践的最大价值之一与调参优势。在一些运动控制问题,如无人机控制以及伺服电机控制,结构上的高频未建模动态不可避免,而 $C_{FL}(s)$ 的低通特性不仅使得调参更加容易(避免了很多高频振荡),也进一步提高了系统低频最大增益的上限(基础增益相对传统 PID 可以调更高)。
二阶 LESO 推导与离散化
回到 $dq$ 轴下的 PMSM 电流方程:
$$
\begin{equation}
\begin{split}
\begin{cases}
\frac{\mathrm{d} i_{d} }{\mathrm{d} t} = -\frac{R_{s}}{L_{d}} i_{d} + \frac{\omega_{e}L_{q}}{L_{d}} i_{q} + \frac{1}{L_{d}} u_{d} \\
\frac{\mathrm{d} i_{q} }{\mathrm{d} t} = -\frac{R_{s}}{L_{q}} i_{q} - \frac{\omega_{e}L_{d}}{L_{q}} i_{d} - \frac{\omega_{e}\psi_{f}}{L_{q}} + \frac{1}{L_{q}} u_{q}
\end{cases}\\
\end{split}
\end{equation}
$$
其中 $i_d$ 和 $i_q$ 分别为状态变量,$u_d$ 和 $u_q$ 分别为控制变量。
-
内部及外部不确定性(非周期性扰动)
以 $d$ 轴方程为例,容易得到非周期性扰动 $f_{dap}$ 可分为已知扰动(known disturbance)$f_{dkn}$、$dq$ 轴耦合项造成的扰动(coupling disturbance)$f_{dco}$,参数失配(parameter perturbation)造成的扰动 $f_{dpa}$,以及其他高次未建模的扰动 $f_{dex}$。即:
$$
\begin{equation}
\begin{split}
\begin{cases}
{f_{dap}}={f_{dkn}}+{f_{dco}}+{f_{dpa}}+{f_{dex}} \\
{f_{dkn}}=-\frac{R_{s0}}{L_{s0}}i_{dc} \\
{f_{dco}}=\omega_{e}i_{qc} \\
{f_{dpa}}=(-\Delta{L_d}\frac{\mathrm{d} i_{dc}}{\mathrm{d} t} - \Delta{R_s}i_{dc} + \omega_e{\Delta{L_q}}i_{qc}) / L_{s0}
\end{cases}\\
\end{split}
\end{equation}
$$对于 $q$ 轴方程:
$$
\begin{equation}
\begin{split}
\begin{cases}
{f_{qap}}={f_{qkn}}+{f_{qco}}+{f_{qpa}}+{f_{qex}} \\
{f_{qkn}}=-\frac{R_{s0}}{L_{s0}}i_{qc} - \frac{\omega_e}{L_{s0}}\psi_{f0} \\
{f_{qco}}=-\omega_{e}i_{dc} \\
{f_{qpa}}=(-\Delta{L_q}\frac{\mathrm{d} i_{qc}}{\mathrm{d} t} - \Delta{R_s}i_{qc} - \omega_e{\Delta{L_d}}i_{dc} - \omega_e{\Delta{\psi_f}}) / L_{s0}
\end{cases}\\
\end{split}
\end{equation}
$$其中 $R_{s0}$ 和 $L_{s0}$、$\psi_{f0}$ 分别为准确的相电阻、相电感、磁链值,而 $\Delta{L_d}=L_d - L_{s0}$,$\Delta{L_q}=L_q - L_{s0}$,$\Delta{R_s}=R_s - R_{s0}$,$\Delta{\psi_{f}}=\psi_{f} - \psi_{f0}$。由此可知,对于凸极性较强的内嵌式永磁同步电机(IPMSM),结构特性导致其 $L_q \ne L_d$,因而 $f_{pa}$ 项的扰动更加明显。
-
周期性扰动(高次谐波脉动)
a) 理想状态下,永磁体磁链波形为正弦波形。在实际情况中,制造误差和气隙可能引入高次磁链谐波,对应到 $qd$ 轴中分别为 $\psi_{dh}$ 和 $\psi_{qh}$。b) 为了避免功率器件(MOS、IGBT 等)在开关时发生上下桥直通短路,通常必须要在 PWM 开关时间中加入死区,但死区时间同时会导致逆变器输出电压波形失真,使得高次谐波含量增加,分别表示为 $u_{dh}$ 和 $u_{qh}$。
c) 周期性扰动 $f_{dp}$、$f_{qp}$ 可表示为下式:
$$
\begin{equation}
\begin{split}
\begin{cases}
f_{dp}=\frac{1}{L_{s0}}(u_{dh} + \omega_{e}\psi_{dh}) \\
f_{qp}=\frac{1}{L_{s0}}(u_{qh} - \omega_{e}\psi_{qh})
\end{cases}\\
\end{split}
\end{equation}
$$
以状态变量 $i_d$ 和 $i_q$、控制变量 $u_d$ 和 $u_q$,考虑上述非周期性和周期性扰动,重写方程,即:
$$
\begin{equation}
\begin{split}
\begin{cases}
\frac{\mathrm{d} i_{d} }{\mathrm{d} t}=b_{0}u_{d} + f_d \\
\frac{\mathrm{d} i_{q} }{\mathrm{d} t}=b_{0}u_{q} + f_q
\end{cases}\\
\end{split}
\end{equation}
$$
其中 $f_d=f_{dap}+f_{dp}$,$f_q=f_{qap}+f_{qp}$。
由上式可得,$dq$ 轴电流微分方程为一阶,适用二阶扩展状态观测器(ESO)来观测扰动。根据 ${[8]}$ 可不加证明地给出电流环二阶 LESO 的表达式,即:
$$
\begin{equation}
\begin{split}
\begin{cases}
e_{1}=z_{1}-x_{1} \\
\dot{z_{1}}=b_{0}u+z_{2}-\beta_{1}e_{1} \\
\dot{z_{2}}=-\beta_{2}e_{1}
\end{cases}\\
\end{split}
\end{equation}
$$
其中 $x_{1}$ 代表状态变量,即测量得到的 $i_{dmeas}$ 或 $i_{qmeas}$,$u$ 代表控制变量 $u_d$ 或 $u_q$,推导出观测器增益 $L^{[8]}$,$\beta_{1} = 2\omega_0$,$\beta_{2} = \omega_{0}^2$。根据电机微分方程,控制增益 $b_0=1/L_{s}$。
采用前向欧拉法对连续域表达式进行离散化处理,以便应用到仿真代码或嵌入式系统中(这一步非常重要):
e1 = z1_prev - x1;
z2_now = z2_prev - (w0 * w0 * e1) * Ts;
z1_now = z1_prev + (b0 * u + z2_prev - 2 * w0 * e1) * Ts;在迭代完成后,再将各先前值 _prev 更新为 _now。
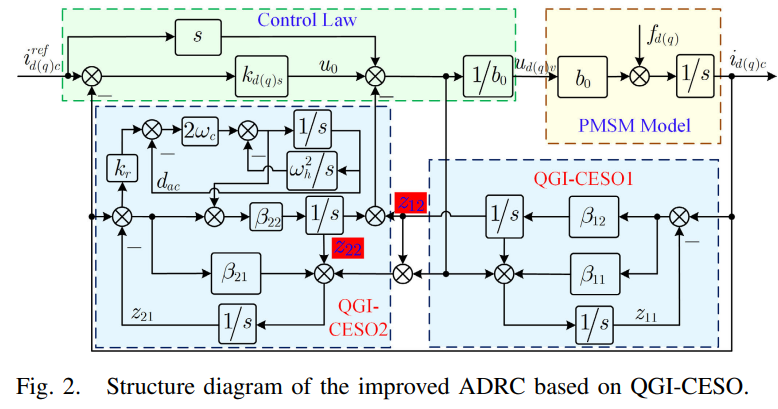
准广义积分器级联型 LESO(QGI-CESO) 推导与离散化
用两个 LESO 去观测误差的级联 LESO 框图$^{[1]}$如下:
在给定斜坡扰动情况下,对比基于单个 LESO 的传统 LADRC 与基于级联 LESO 的增强型 LADRC 的估计扰动误差$^{[9]}$如下:
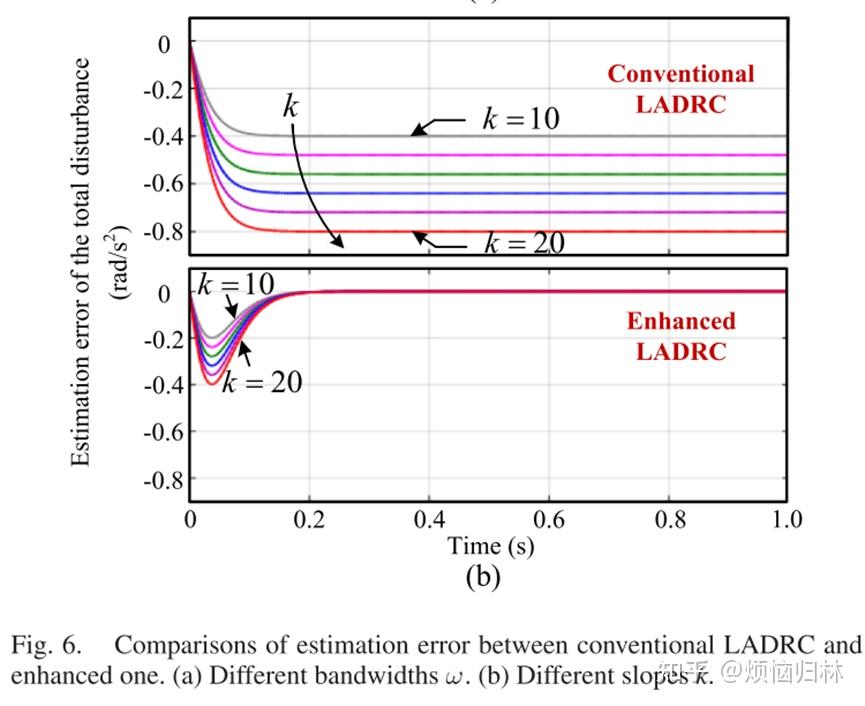
可以看到,单个 LESO 无法有效跟踪斜坡扰动,单个 LESO 估计的扰动数值会和实际扰动存在一个直流静差;斜坡扰动越大,单个 LESO 估计的误差越大。同时可以发现,级联 LESO 可以有效跟踪斜坡扰动。这一点是很好解释的。
可以这么理解,用单个 LESO 去跟随一个斜坡扰动之后,还会剩下一个直流扰动无法被有效抑制,这时候再串联一个 LESO,就可以把剩下的直流扰动抑制了(用单个 LESO 跟随直流扰动当然是没问题的)。
PS:基于 CESO 的方法比传统的 ESO 具有更好的低频扰动估计能力,并且二者的高频特性是一致的。$^{[9]}$
QGI-CESO1 与二阶 LESO 相同,此处略过。
给出 QGI-CESO2 的表达式:
$$
\begin{equation}
\begin{split}
\begin{cases}
e_{21}=z_{21}-x_{1} \\
\dot{z_{21}}=b_{0}u+z_{12}+z_{22}-\beta_{21}e_{21} \\
\dot{z_{22}}=\beta_{22}\dot{d_{ac}} -\beta_{22}e_{21} \\
\dot{d_{ac}}=-2\omega_{c}d_{ac} + 2k_{r}\omega_{c}e_{21} + m \\
\dot{m}=-\omega_{h}^2d_{ac}
\end{cases}\\
\end{split}
\end{equation}
$$
其中 $d_{ac}$ 为电流高次谐波分量,$k_{r}$ 为 QGI 增益,$w_{h}$ 为主要谐波频率。
仍采用前向欧拉法进行离散化:
e21 = z21_prev - i_real;
m_now = m_prev - (wh * wh * dac_prev) * Ts;
dac_dot = (-2 * wc * dac_prev + 2 * kr * wc * e21 + m_prev);
dac_now = dac_prev + dac_dot * Ts;
z22_now = z22_prev + (wo * wo * dac_dot - wo * wo * e21) * Ts;
z21_now = z21_prev + (b0 * u + z12_prev + z22_prev - 2 * wo * e21) * Ts;
e11 = z11_prev - i_real;
z12_now = z12_prev - (wo * wo * e11) * Ts;
z11_now = z11_prev + (b0 * u + z12_prev - 2 * wo * e11) * Ts;参数选取:
- $\beta_{1i}=\beta_{2i}=\frac{2!}{(2-i)!*i!}w_0^i$,根据二阶 LESO 推导得,$\beta_{11}=\beta_{21}=2\omega_0$,$\beta_{12}=\beta_{22}=\omega_0^2$。
- QGI 增益 $K_r$ 取 5~15$^{[1]}$,我们取 $K_r=10$。当 $K_r=0$ 时,QGI-CESO 退化为传统级联型 ESO(CESO)。
- 观测器带宽 $\omega_0=5\sim10{\omega_n}$,其中 $\omega_n$ 为电流环带宽。
- 谐波频率 $\omega_h$ = 6 倍基频 $6\omega_e$,基波频率 $\omega_e=\frac{n}{60}n_p$(单位 rad/s),其中 $n$ 为电机机械转速(单位 RPM),$n_p$ 为电机极对数。QGI 截止频率 $\omega_c=0.5\%\sim 15\%\omega_h$。
CESO 输出总扰动 $\hat{f_q} = \hat{x_2} = z_{12} + z_{22}$。
Simulink 模块框图如图所示:
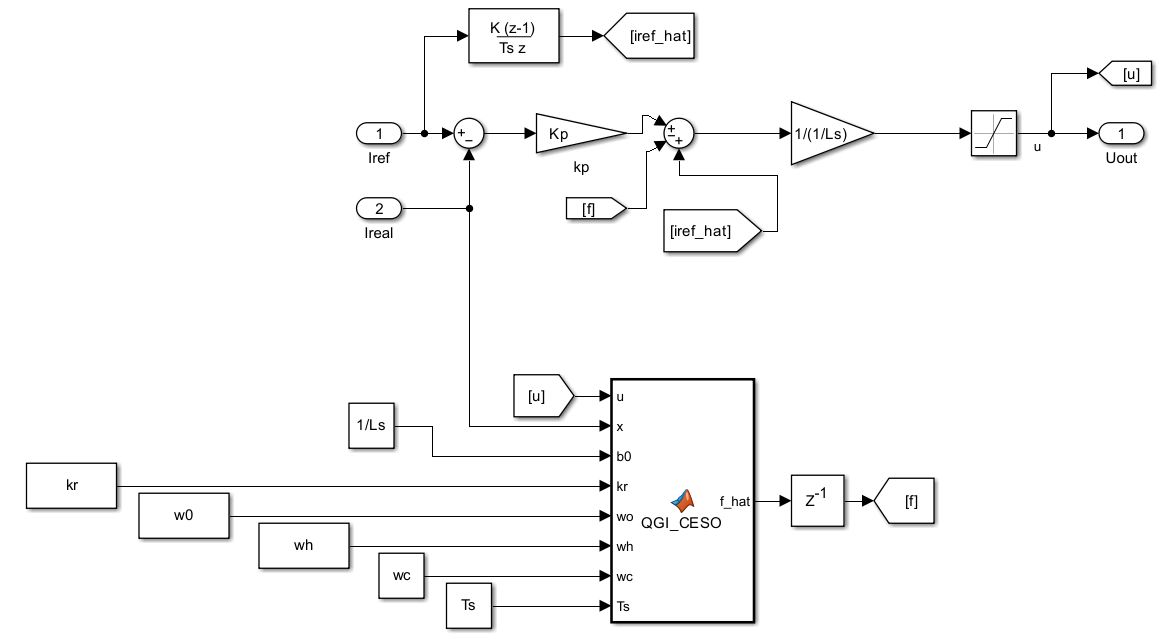
仿真验证
仿真参数
Tstep = 5e-07; % powergui 仿真步长
Tpwm = 0.0001; % PWM 开关周期
Tsample = Tpwm; % 采样周期(单采单更)
Tspeed = 5 * Tsample; % 转速采样周期
Pn = 4; % 电机极对数
Ls = 0.0085; % 相电感,Ld = Lq = Ls
Rs = 3; % 相电阻
flux = 0.1688; % 永磁体磁链
Tdead = 0; % 死区时间
J = 0.01; % 转动惯量
B = 2e-3; % 阻尼系数
n_init = 0; % 初始转速仿真工况
空载启动至 1000RPM,0.2s 突加 10Nm 负载,0.4s 参考转速改为 500RPM,四对极电机,500RPM 下基波频率 $\omega_e$ 为(500/60)*4=33.33Hz
采用一阶 LADRC 作为转速环,分别采用 PI 电流环、一阶 LADRC(为避免不必要的相位滞后,省略了跟踪微分器)、改进型 LADRC 作为电流环,对比运行效果。其中 PI 控制器的带宽设置为 10K,$K_p$、$K_i$ 采用上述方法根据 $R_s$、$L_s$ 进行整定;一阶 LADRC 和改进型 LADRC 的观测器带宽 $\omega_0$ 为 10K,控制带宽 $\omega_c$ 为 2.5K;改进型 LADRC,谐波频率 $\omega_h$ 设置为基波频率 $\omega_e$ 的 6 倍。
转速、转矩、三相电流对比
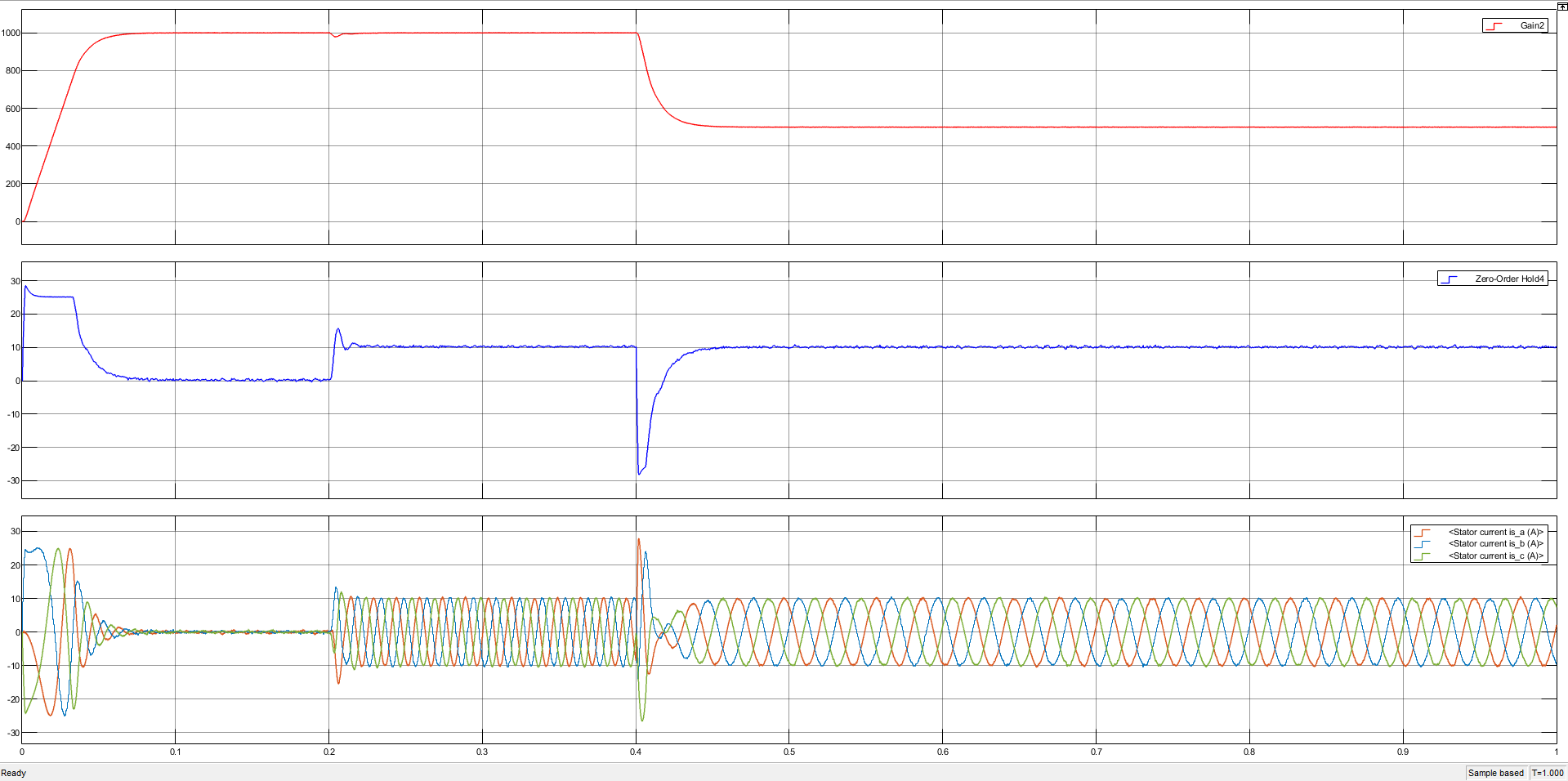
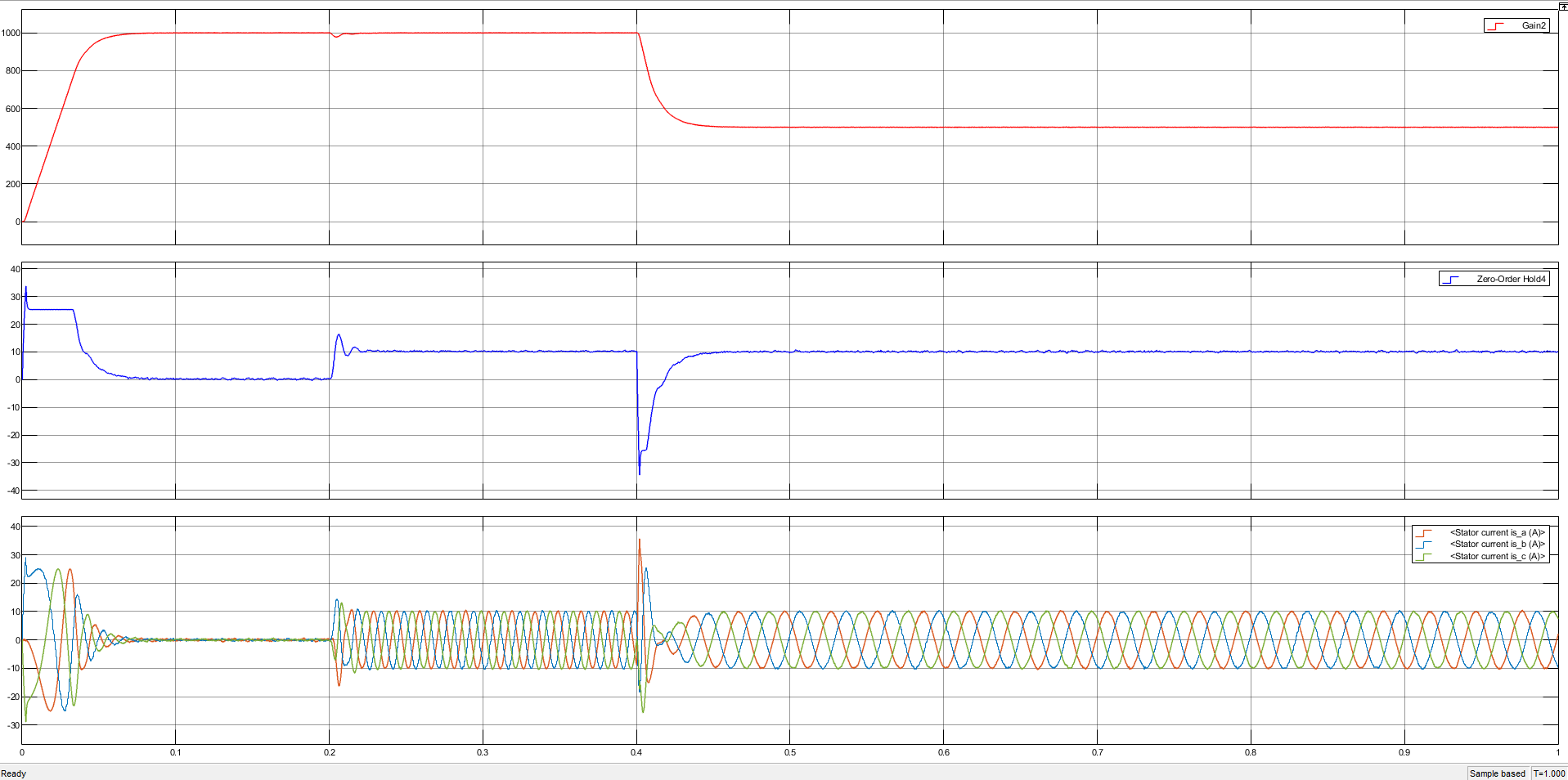
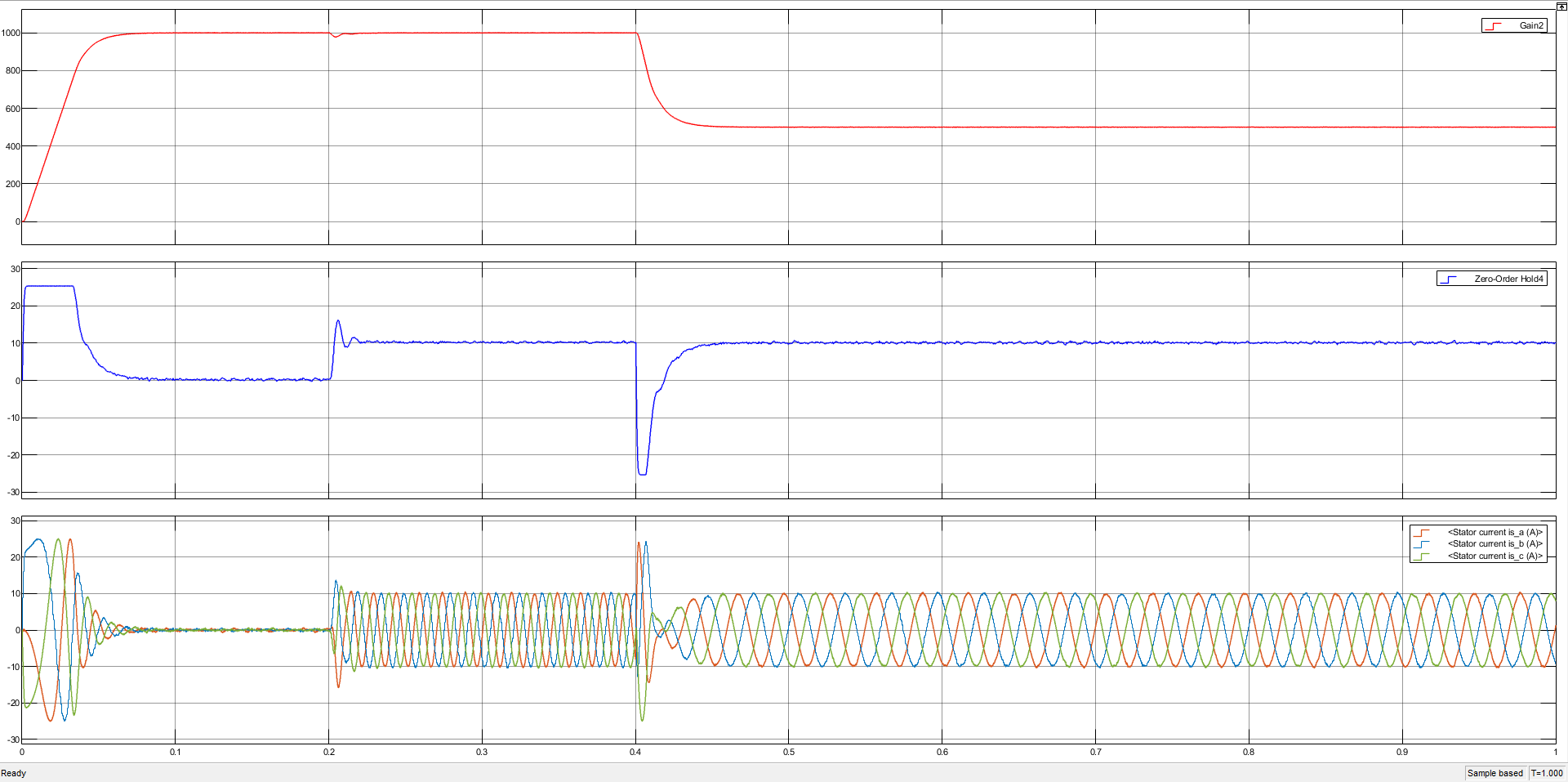
三种电流环控制器在转速保持方面,由于转速环采用无超调的 LADRC 控制器,表现均良好。转矩方面,PI 控制器不出所料,在突加阶跃电压输入下转矩产生了过冲;而一阶 LADRC 可能是省去了跟踪微分器的原因,在相对较高的带宽下突加/突减载荷过冲更加明显。改进型 LADRC 的转矩没有发生过冲。
dq 轴电流波形对比
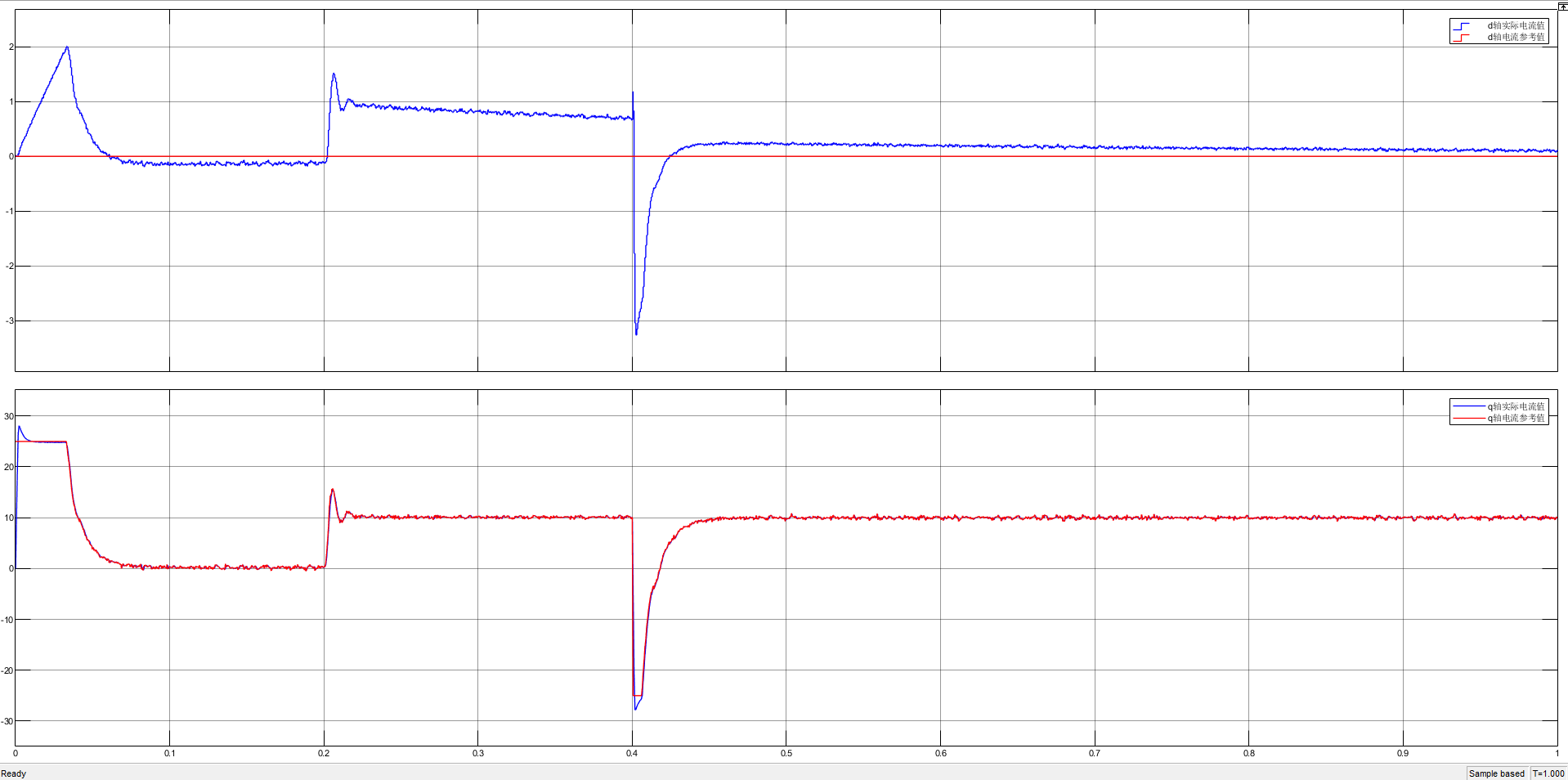

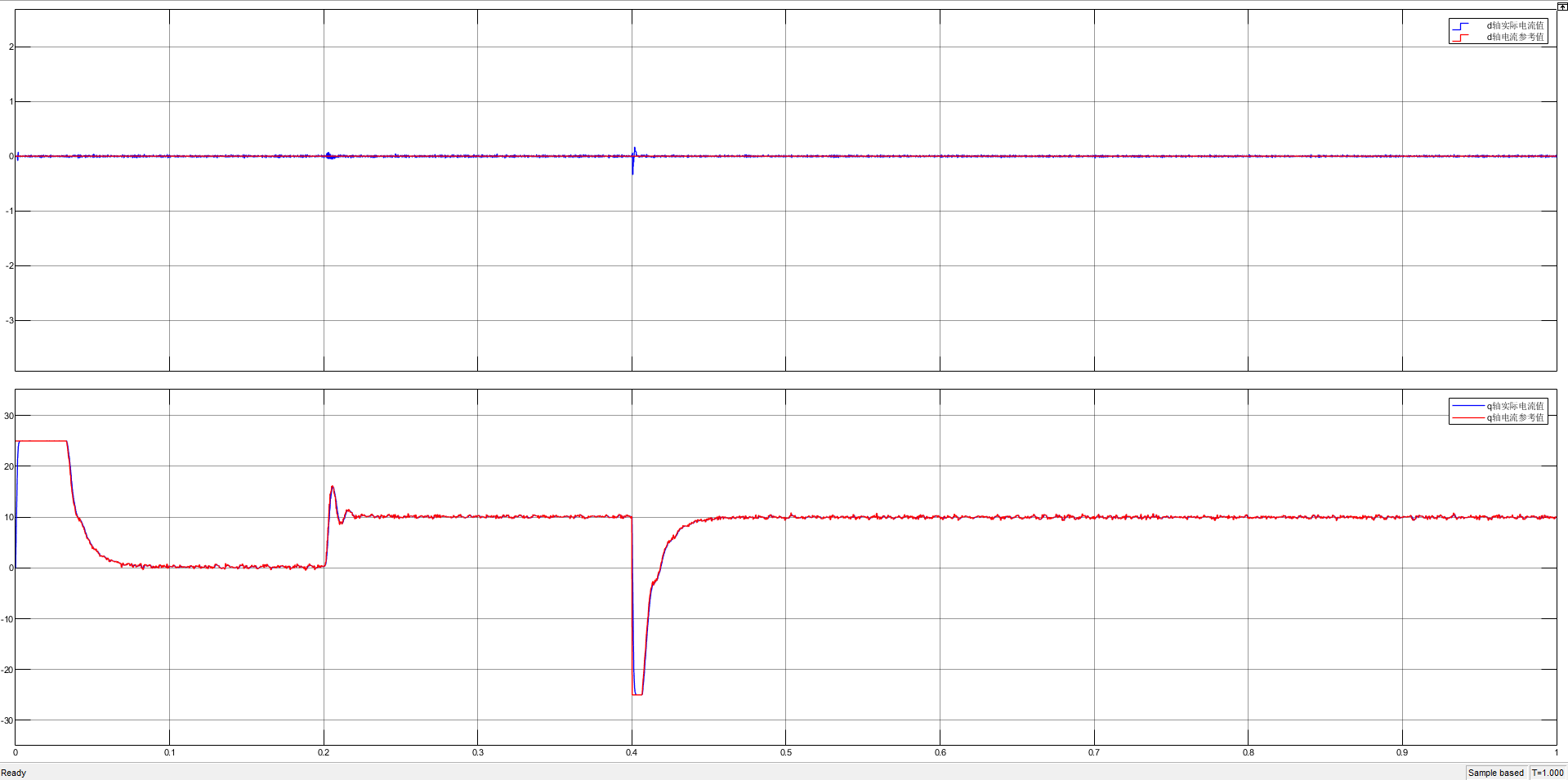
相同比例尺下 D 轴电流对比非常明显:PI 电流环在受到外部扰动时不管是 Q 轴还是 D 轴均偏移较大并产生超调,D 轴还疑似受到耦合项误差干扰,并且可能是积分增益调节原因,偏移量恢复较慢;一阶 LADRC 电流环电流波动幅度较大,但相比于 PI 电流环能更快的回到参考值,此外在 0.1s ~ 0.2s、0.2s ~ 0.4s 时间段中,可以明显看到一阶 LADRC 对于斜坡扰动的跟踪是存在直流误差的;对于改进型级联 LADRC 电流环,D 轴的扰动抑制、谐波抑制效果都体现得很明显。
稳态电流 THD 对比
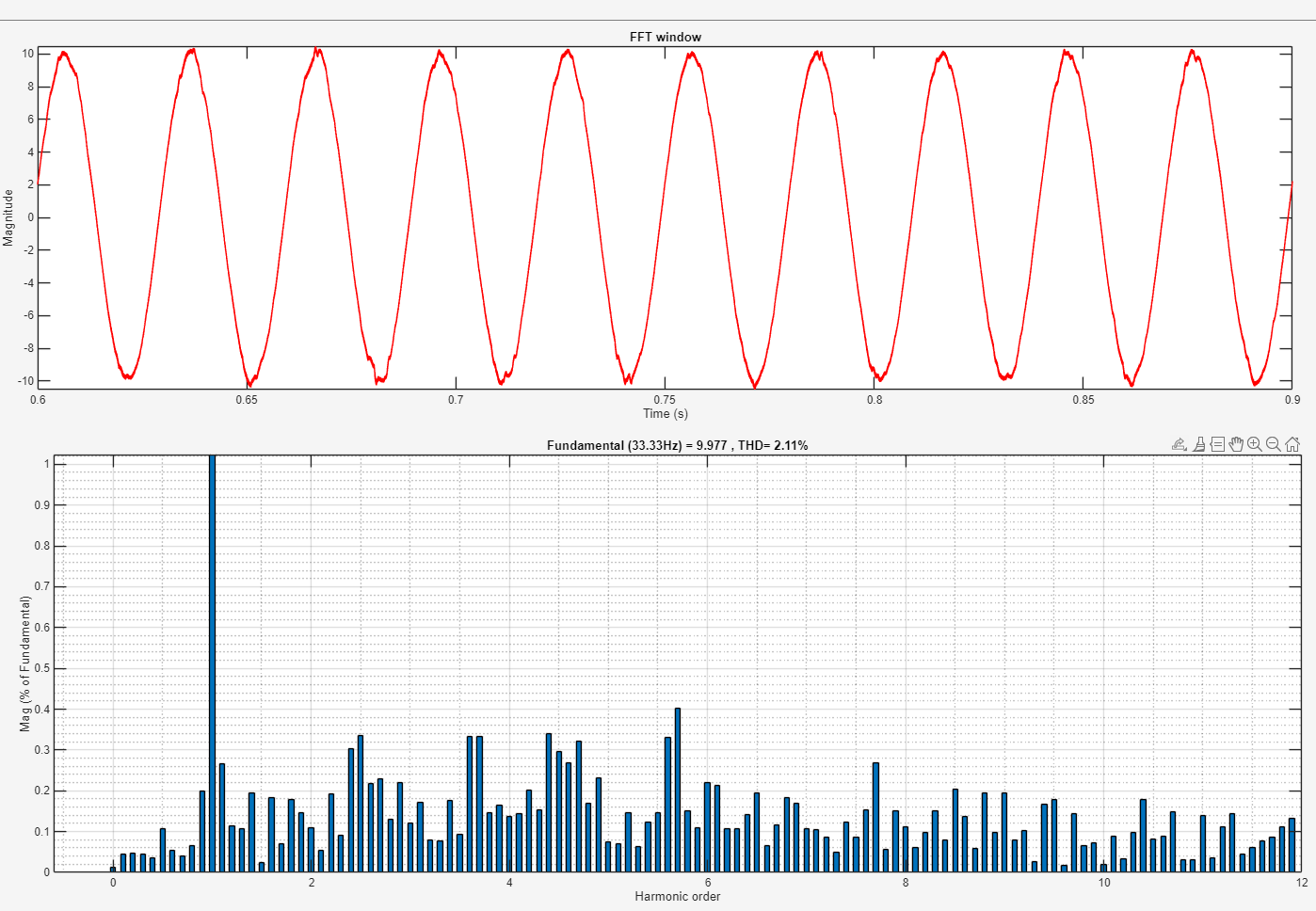

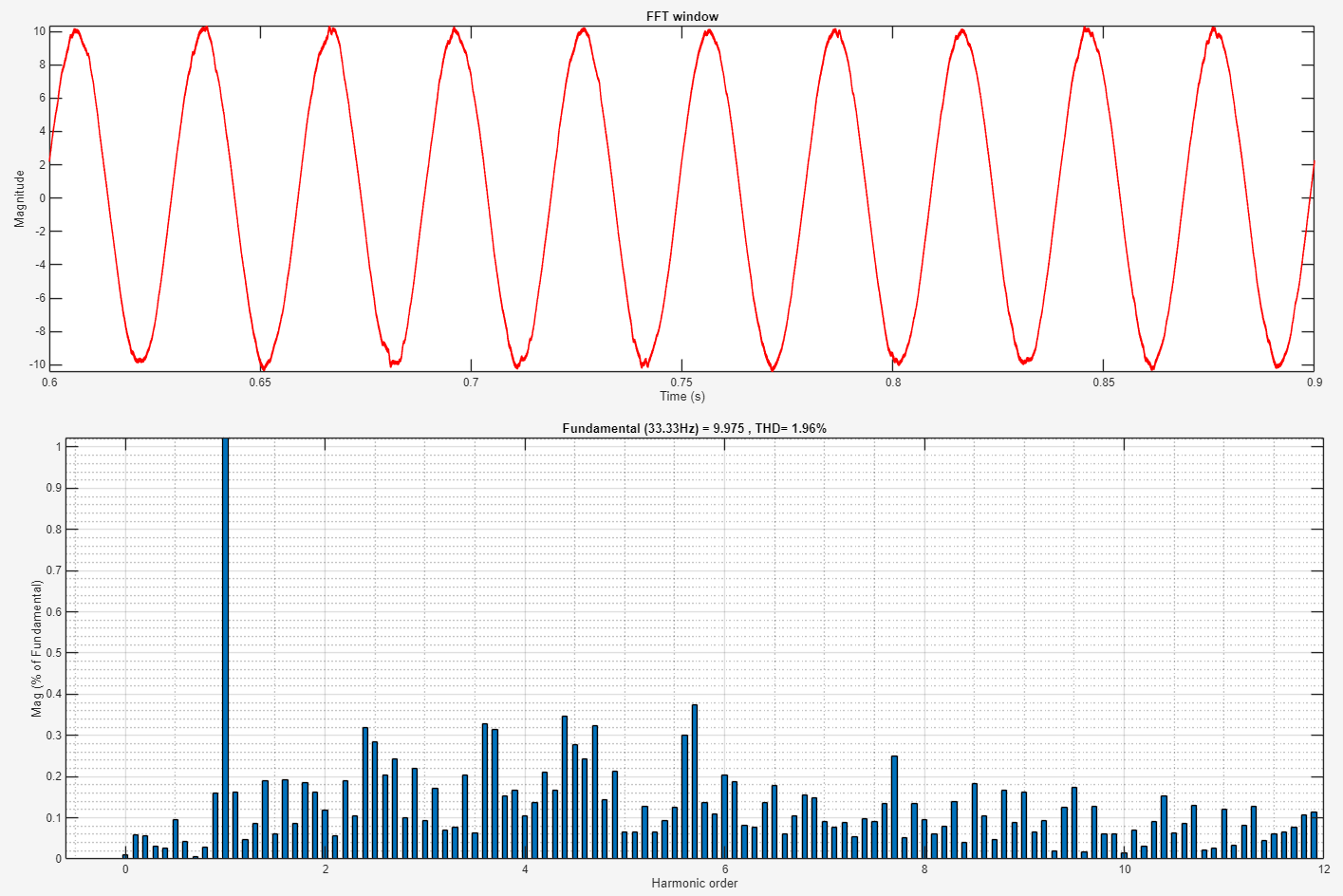
三种电流环的 THD 依次降低,可能是因为仿真参数中没有加入死区时间,因而改进 LADRC 对高次谐波的抑制效果不是很明显。后期应继续改进实验方法,并准备在嵌入式实机平台上进行实验验证。
参考资料
[2] 永磁同步电机矢量控制(三)——电流环转速环 PI 参数整定
[3] 永磁同步电机矢量控制(FOC)—电流环及速度环PI参数整定
